Sarvesh K Verma Solutions for Chapter: Mensuration, Exercise 9: Test of Your Learning

A cube of maximum possible volume is cut from the solid right circular cylinder. What is the ratio of volume of cube to that of cylinder if the edge of a cube is equal to the height of the cylinder?

In a right angle triangle $\mathrm{ABC}$, what is the maximum possible area of a square that can be inscribed when one of its vertices coincide with the vertex of the right angle of the triangle?

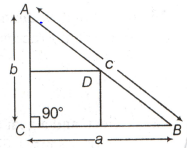
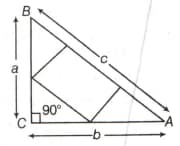
In the adjoining figure, a square of maximum possible area is circumscribed by the right-angle triangle $\mathrm{ABC}$ in such a way that one of its sides just lies on the hypotenuse of the triangle. What is the area of the square?

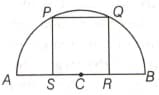
In the adjoining figure P Q R S is a square of maximum possible area which is circumscribed by the semicircle. Points R and S lie on the diameter A  B. What is the area of the square if the radius of the circle is ' r ?

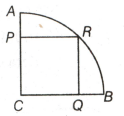
In the adjoining figure a quadrant (of circle) inscribes a square of maximum possible area. If the radius of the circle be ' $r$ ' then what is the area of the square?

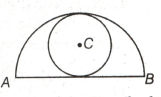
In the adjoining figure, $\mathrm{AB}$ is the diameter of a semicircle which inscribes a circle of maximum possible area. If the radius of the larger circle (i.e., semicircle) is $\mathrm{r}$, the area of the inscribed circle is:

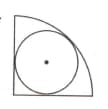
In a quadrant (of a circle) a circle of maximum possible area is given. If the radius of the circumscribing quadrant be r, then what is the area of the inscribed circle?

A cylindrical chocobar has its radius $\text{'}\mathrm{r}\text{'}$ unit and height $\text{'}\mathrm{h}\text{'}$ unit. If we wish to increase the volume by the same unit either by increasing its radius alone or its height alone, then how many units do we have to increase the radius or height?